Hello Everyone!! Hope everyone is doing ok, the previous semester was pretty hectic with research work and courses so didn’t really have time to write anything up. But now I’m back and in todays post I thought of writing something interesting I learned in a course and something that apparently ends up being a common interview question for coding/developing positions–that is to "identify cycles in a linked list". If you are from a CS background, you’d probably know that job interviews usually consist of a couple of problems which test a candidates knowledge on algorithms & data structures. If you just stumbled across my post and if you had no idea of this, well now you know.
Anyways, without digressing anymore back to my topic–linked lists are a basic data structure like arrays which are used quite a lot. Now if you have no idea about linked lists and you want to learn about them then this is not the post for that. There are lots of youtube tutorials and posts online which would probably give you a fair understanding on how this data structure works. Click on these links to learn more about linked lists - [youtube], [weblink]
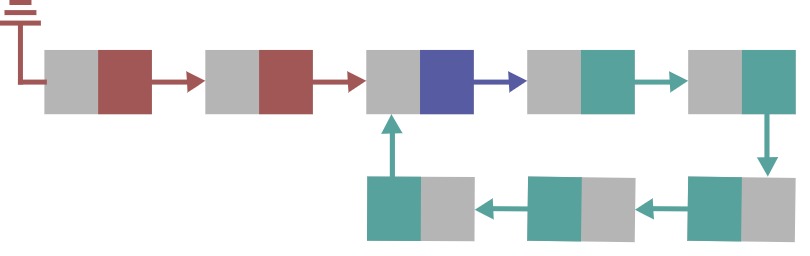
The problem : a cyclic linked list
Now to our problem at hand. I’m assuming you know how a link list works, so basically as depicted above each link would have some storage capability to store data and a pointer to the next link which is the arrow. So if you look at the image above, the linked list starts from the red link at the left end and moves to the right. If you follow through the connectivity of this linked list starting form the red links shown in the image above you would notice that the traversal itself would never stop. Because the green pointer (the arrow) of the list would point again to the blue link which in-turn points back to the green links.
This would be a nightmare in real code because the code will run in an infinite loop. And the worst part is its caused because of the connectivity of the underlining data structure and not an issue with the core programing logic, so figuring it out could be tricky also. But as it turns out there is a simple algorithm that can check if there are any cycles in a linked list.
// definition for a Node in a link list
typedef struct Node{
Data value; // the data structure
struct Node * next; // pointer to next node
}Node;
// definition of the linked list
typedef struct Linkedlist{
Node * head;
}Linkedlist;
Lets consider the above basic C declarations for a Node (link) and the linked list. I’ll be explaining the working algorithm using a C skeleton code so I’m again assuming you have some working knowledge of C and pointers. If you don’t know much about this, think of Node and Linkedlist as two classes where the linked list has a reference to its head (i.e. its starting location) and each Node has a reference to the data and the Node connected to it.
Cycle detection algorithm
int detectCycle(Linkedlist * l)
{
if (l->head == NULL) return 0;
Node * s = l->head , * f1 = l->head;
Node * f2 = f1->next;
while (s && f1 && f2) {
s = s->next;
f1 = f2->next;
if (f1 != NULL) f2 = f1->next;
if (s == f1 || s == f2) return 1;
}
return 0;
}
The algorithm itself isn’t pretty long right? But how does this work? I’ll explain that next. First of all the algorithm checks if l->head == NULL which indicates if the linked list is empty or not, if it’s empty then it returns 0 meaning there is no cycle. The algorithm works on the three pointers s, f1 and f2 which means start, fast1 and fast2. These pointers reference some node in the link list. Initially both the pointers of s and f1 point to the head of the linked list while f2 refers to the node right after the head. The idea is very simple, at every instance of the while loop the pointers f1, f2 are moved forward in the list by two positions while the pointer s is moved by one position. (Now you might notice the reason ‘f1,f2’ are named fast is because these pointers traverse the list faster than ‘s’) Given there is a cycle then at some point f1 == s OR f2 == s then the algorithm returns 1 else if any of the pointers finish traversing the list it returns 0.
Lets work this out for the linked list drawn above, I will name each node with a number from 1-8 where the first red node to the left is 1 and the final green node 8. In the table below I’ll show the position of the pointers at each step of the while loop.
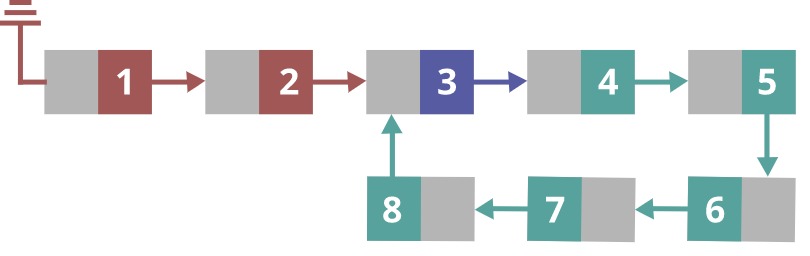
| timestep | pointer s | pointer f1 | pointer f2 |
| Initially | 1 (head) | 1 (head) | 2 |
| step 1 | 2 | 3 | 4 |
| step 2 | 3 | 5 | 6 |
| step 3 | 4 | 7 | 8 |
| step 4 | 5 | 3 | 4 |
| step 5 | 6 | 5 | 6 |
At step 5 f2 == s which means there is a cycle. So there you go, a simple algorithm to identify cycles in linked lists.
So until next time,
Cheers!
Next: Adding git support to Terminal
Prev: Markov Chains 101